Alur Kerja Ant Colony Optimization (ACO)

Ulasan Penjelasan

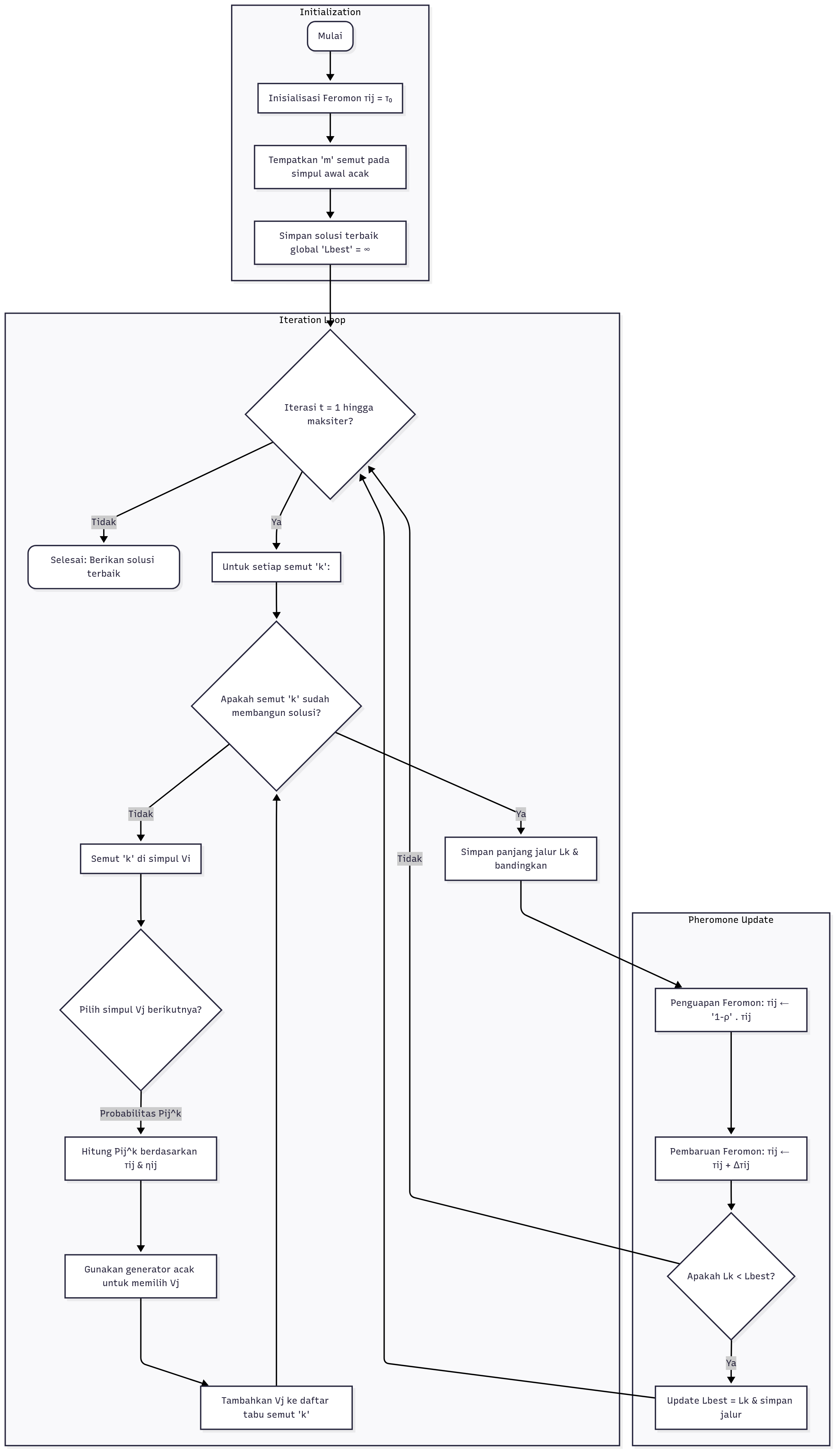
Algoritma Ant Colony Optimization (ACO) bekerja melalui serangkaian langkah yang berulang (iterasi) untuk menemukan jalur optimal dalam sebuah graph. Berikut adalah alur kerja lengkapnya.

1. Inisialisasi

Pada langkah ini, semua parameter dan struktur data disiapkan:

• Waktu t=0: Iterasi dimulai.
• Inisialisasi Feromon: Setiap edge (e_ij) antara simpul V_i dan V_j diberi nilai feromon awal (τ_ij) yang sama dan konstan, biasanya τ₀ = konstanta kecil.
• Penempatan Semut: Sebanyak m semut ditempatkan pada simpul-simpul awal, yang bisa ditentukan secara acak atau pada satu simpul tertentu. Setiap semut memiliki memori (disebut daftar tabu) untuk mencatat simpul yang telah dikunjunginya.

2. Siklus Konstruksi Solusi

Pada setiap iterasi, semua semut secara paralel membangun sebuah solusi.

• Pemilihan Jalur: Setiap semut k yang berada di simpul V_i memilih simpul berikutnya (V_j) untuk dikunjungi. Pemilihan ini bersifat probabilistik dan didasarkan pada dua faktor:
  1. Feromon (τ_ij): Jumlah feromon pada edge e_ij. Semakin banyak feromon, semakin tinggi daya tariknya.
  2. Informasi Heuristik (η_ij): Biasanya adalah kebalikan dari jarak (1/d_ij) atau biaya edge tersebut. Semakin pendek jarak, semakin tinggi daya tariknya.

Probabilitas semut k untuk bergerak dari V_i ke V_j dihitung dengan rumus:

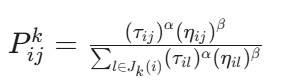
Di sini, J_k(i) adalah himpunan simpul yang belum dikunjungi oleh semut k.

3. Pembaruan Global Feromon

Setelah semua semut menyelesaikan solusinya, nilai feromon pada semua edge diperbarui secara global.

• Penguapan Feromon (Evaporation): Semua feromon pada setiap edge dikurangi dengan tingkat penguapan (ρ). Ini mencegah jalur yang kurang baik menjadi terlalu dominan. Rumusnya:
  
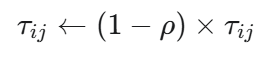
• Penyetoran Feromon (Deposition): Feromon baru ditambahkan pada edge yang dilewati oleh semut, biasanya dengan prioritas pada jalur terbaik. Rumusnya:
  

Di mana Δτ^k_ij adalah jumlah feromon yang disumbangkan oleh semut k: k.(Q/L_k , di mana L_k adalah panjang jalur semut k). . Semut dengan jalur terpendek akan menyumbang feromon paling banyak.

4. Kondisi Berhenti (Termination)

Langkah 2 dan 3 terus diulang hingga salah satu kondisi berhenti terpenuhi, seperti:

• Mencapai jumlah iterasi maksimum yang telah ditentukan.
• Tidak ada perbaikan yang signifikan pada solusi terbaik selama beberapa iterasi.
• Mencapai batas waktu komputasi.

Setelah kondisi berhenti terpenuhi, algoritma akan menampilkan solusi terbaik yang telah ditemukan.