🎯 Definisi Algoritma

"Dalam riset, setiap pilihan desain harus punya alasan yang kuat. Tidak ada yang random, semua berdasarkan hipotesis dan scientific reasoning."

Flowchart Alur Kerja Algoritma ACO untuk TSP/MST

1️⃣ Penjelasan Algoritma/Metode

📌 Algoritma Ant Colony Optimization (ACO)

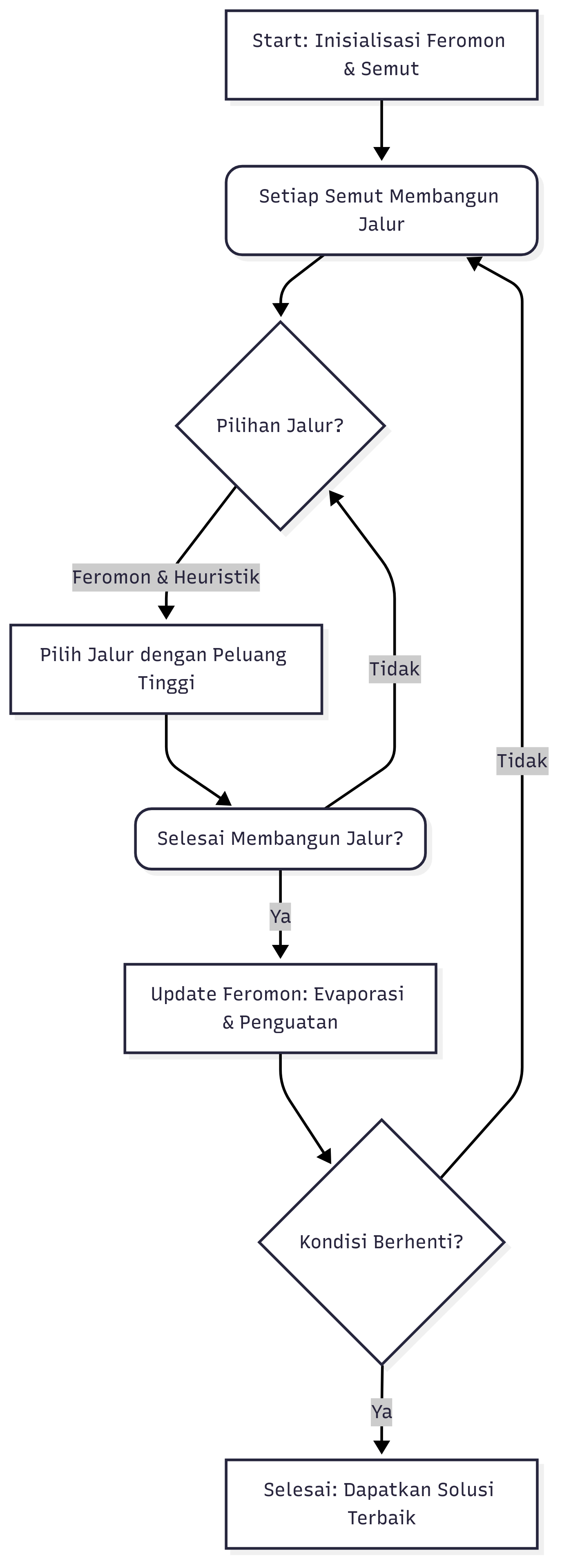
Algoritma ACO adalah metode heuristik probabilistik yang terinspirasi dari perilaku semut dalam mencari jalur terpendek dari sarang menuju sumber makanan. Ide dasarnya adalah semut akan melepaskan jejak feromon di sepanjang jalur yang mereka lalui. Semakin banyak semut yang melewati suatu jalur, semakin kuat jejak feromonnya. Semut lain akan cenderung mengikuti jalur dengan jejak feromon terkuat. Mekanisme ini menciptakan umpan balik positif yang secara bertahap mengarahkan sebagian besar semut menuju jalur yang optimal.

Cara Kerja ACO (General):

Inisialisasi: Semut ditempatkan secara acak pada beberapa simpul. Feromon pada setiap jalur (edge) diinisialisasi dengan nilai yang sama.
Konstruksi Solusi: Setiap semut secara mandiri membangun sebuah jalur (solusi) dengan berpindah dari satu simpul ke simpul lainnya. Pilihan jalur bergantung pada dua faktor: Nilai Feromon dan Informasi Heuristik (misalnya, jarak antar simpul).
Penguapan Feromon (Pheromone Evaporation): Setelah semua semut menyelesaikan jalurnya, nilai feromon pada semua jalur akan menguap. Ini mencegah algoritma terjebak pada solusi yang suboptimal dan memungkinkan eksplorasi jalur baru.
Pembaruan Feromon (Pheromone Update): Semut yang menemukan solusi terbaik (misalnya, jalur terpendek) akan memperkuat jejak feromon pada jalur yang mereka lalui. Ini adalah mekanisme umpan balik positif yang mendorong konvergensi algoritma.
Iterasi: Langkah-langkah ini diulang sampai kondisi berhenti terpenuhi, seperti mencapai jumlah iterasi maksimum atau menemukan solusi yang stabil.

📌 Algoritma Kruskal (untuk Minimum Spanning Tree)

Algoritma Kruskal adalah salah satu algoritma serakah (greedy) yang paling umum digunakan untuk menemukan Minimum Spanning Tree (MST). Sebuah spanning tree dari sebuah graph adalah sub-graph yang mencakup semua simpul asli, tetapi tidak memiliki siklus. MST adalah spanning tree dengan total berat (weight) edge yang paling kecil. Algoritma ini disebut "serakah" karena pada setiap langkah, ia memilih edge dengan berat terkecil yang tersedia.

Cara Kerja Kruskal:

Pengurutan: Urutkan semua edge dalam graph secara menaik (dari berat terkecil ke terbesar).
Inisialisasi: Buat sebuah set kosong untuk MST dan setiap simpul menjadi setnya sendiri (disjoint set).
Iterasi & Pemilihan Edge: Ambil edge dengan berat terkecil dari daftar yang sudah diurutkan.
Pemeriksaan Siklus: Periksa apakah edge yang dipilih menghubungkan dua simpul yang sudah berada dalam set yang sama. Jika ya, abaikan edge tersebut.
Penggabungan: Jika edge yang dipilih menghubungkan dua simpul yang berada di set yang berbeda, tambahkan edge tersebut ke MST dan gabungkan kedua set simpul.
Kondisi Berhenti: Ulangi langkah-langkah di atas hingga MST memiliki $V-1$ edge, di mana $V$ adalah jumlah simpul dalam graph.

2️⃣ Perbedaan Kunci: ACO-TSP vs. ACO-MST

Meskipun ACO dapat diterapkan pada berbagai masalah, ada perbedaan fundamental dalam cara kerja untuk TSP (Travelling Salesman Problem) dan MST (Minimum Spanning Tree).

ACO-TSP: Bertujuan menemukan jalur Hamiltonian terpendek, yaitu jalur yang mengunjungi setiap simpul tepat satu kali dan kembali ke simpul awal untuk membentuk sebuah siklus. Semut dalam algoritma ini sengaja membangun siklus, dan memori (tabu list) digunakan untuk mencegah kunjungan ganda pada simpul yang sama.
ACO-MST: Bertujuan menemukan spanning tree dengan total bobot minimum. Dalam proses konstruksi solusinya, semut harus menghindari siklus sama sekali. Konsepnya adalah memilih edge dari daftar edge yang valid yang tidak akan membuat siklus.

3️⃣ Mengapa Ide-Ide Ini Muncul? (Scientific Reasoning)

💡 Design Thinking Process:

Dalam riset ini, pemilihan algoritma dan metode memiliki alasan yang jelas, yang berakar pada metodologi ilmiah.

Step 1: Establish Ground Truth

Memilih Kruskal sebagai Gold Standard yang guaranteed optimal. Ini berfungsi sebagai tolok ukur untuk mengukur seberapa baik kinerja algoritma heuristik.

Step 2: Test Basic Heuristic

Menguji ACO dengan parameter standar untuk mendapatkan baseline performa. Ini menjadi titik awal untuk perbandingan.

Step 3: Hypothesis Testing (Parameter Tuning)

Menyelidiki apakah penyetelan parameter ACO dapat meningkatkan performa. Ini adalah esensi dari metode ilmiah, yaitu menguji hipotesis melalui eksperimen.

Step 4: Problem Variation (TSP vs MST)

Membandingkan performa ACO pada dua masalah yang berbeda (TSP dan MST) untuk menguji kemampuan generalisasi algoritma.

Step 5: Real-World Constraint

Mengimplementasikan batasan derajat (degree constraint) untuk melihat seberapa tangguh (robust) ACO dalam menghadapi skenario dunia nyata yang tidak ideal.

4️⃣ Filosofi: Ilmu Pasti vs Ilmu Heuristik

🤔 Mengapa Perlu Ilmu Pasti di Heuristik?

Heuristik sering dianggap "tidak pasti", namun validasi ilmiah sangatlah penting.

Validasi: Tanpa solusi pasti (seperti dari Kruskal), kita tidak bisa mengetahui seberapa bagus sebuah heuristik. Heuristik tanpa validasi adalah tebak-tebakan.
Benchmarking: Membutuhkan tolok ukur untuk mengukur perbaikan. Mengatakan "ACO 5% dari optimal" lebih bermakna daripada "ACO dapat 1000".
Memahami Trade-offs: Memungkinkan kita untuk mengukur kompromi antara akurasi dan kecepatan, misalnya "10x lebih cepat, 5% kurang akurat".

"Heuristik yang baik adalah yang tahu kapan dia gagal. Dan itu hanya bisa diketahui dengan membandingkan dengan solusi pasti."

5️⃣ Harapan & Future Direction

Arah riset ke depan dapat mencakup:

Algoritma Hibrida: Menggabungkan algoritma pasti dengan heuristik untuk mendapatkan yang terbaik dari kedua dunia.
Heuristik Adaptif: Algoritma yang dapat menyetel parameternya sendiri secara otomatis tanpa intervensi manual.
Aplikasi Praktis: Menerapkan heuristik yang dapat diskalakan (scalable) untuk masalah Big Data dan real-time optimization.

📊 Contoh Perhitungan Manual ACO Step-by-Step

🗺️ Setup: Graph Sederhana 4 Nodes

Graph:

    A ----10---- B
    |           /|
   20         15 |
    |       /    |5
    |     /      |
    C --12---- D

Distance Matrix:

	A	B	C	D
A	0	10	20	∞
B	10	0	15	5
C	20	15	0	12
D	∞	5	12	0

Parameter ACO:

α (alpha) = 1 - bobot pheromone
β (beta) = 2 - bobot heuristic
ρ (rho) = 0.5 - evaporation rate
Q = 100 - konstanta pheromone
τ₀ (tau initial) = 1 - pheromone awal

🐜 ITERATION 1 - SEMUT 1

Inisialisasi

Pheromone awal: τ = 1 untuk semua edge

Edge	τ (Pheromone)
A-B	1.0
A-C	1.0
B-C	1.0
B-D	1.0
C-D	1.0

Start: Node A (random)

Step 1: Dari A, pilih edge berikutnya

Kandidat edge: A-B, A-C

Hitung Heuristic (η = 1/distance):

η_AB = 1/10 = 0.100
η_AC = 1/20 = 0.050

Hitung Attractiveness (τ^α × η^β):

τ^α × η^β = τ¹ × η²

Edge	τ	η	τ¹ × η²	Calculation
A-B	1	0.100	0.0100	1 × 0.100² = 0.0100
A-C	1	0.050	0.0025	1 × 0.050² = 0.0025

Hitung Probabilitas:

Total attractiveness: 0.0100 + 0.0025 = 0.0125

P_AB = 0.0100 / 0.0125 = 0.80 (80%)
P_AC = 0.0025 / 0.0125 = 0.20 (20%)

✅ Pilih: A-B (probabilitas tertinggi)
Path sekarang: A → B

Step 2: Dari B, pilih edge berikutnya

Kandidat edge: B-C, B-D (A sudah dikunjungi)

Hitung Heuristic:

η_BC = 1/15 = 0.067
η_BD = 1/5 = 0.200

Hitung Attractiveness:

Edge	τ	η	τ¹ × η²
B-C	1	0.067	0.0045
B-D	1	0.200	0.0400

Hitung Probabilitas:

Total: 0.0045 + 0.0400 = 0.0445

P_BC = 0.0045 / 0.0445 = 0.10 (10%)
P_BD = 0.0400 / 0.0445 = 0.90 (90%)

✅ Pilih: B-D (lebih pendek, probabilitas tinggi)
Path sekarang: A → B → D

Step 3: Dari D, pilih edge berikutnya

Kandidat edge: D-C (A, B sudah dikunjungi)

Hanya 1 pilihan → probabilitas 100%

✅ Pilih: D-C
Path final: A → B → D → C
Total distance: 10 + 5 + 12 = 27

♻️ UPDATE PHEROMONE (Setelah Semut 1)

Step 1: Evaporation (Semua Edge)

τ_new = (1 - ρ) × τ_old = (1 - 0.5) × τ_old = 0.5 × τ_old

Edge	τ_old	Evaporation	τ_{after evap}
A-B	1.0	0.5 × 1.0	0.5
A-C	1.0	0.5 × 1.0	0.5
B-C	1.0	0.5 × 1.0	0.5
B-D	1.0	0.5 × 1.0	0.5
C-D	1.0	0.5 × 1.0	0.5

Step 2: Deposit (Hanya Edge yang Dilalui)

Path Semut 1: A-B, B-D, D-C

Total distance (L): 27

Δτ = Q / L = 100 / 27 = 3.704

Edge	τ_{after evap}	Dilalui?	Δτ	τ_final
A-B	0.5	✓ Ya	3.704	4.204
A-C	0.5	✗ Tidak	0	0.5
B-C	0.5	✗ Tidak	0	0.5
B-D	0.5	✓ Ya	3.704	4.204
C-D	0.5	✓ Ya	3.704	4.204

📊 Hasil Iteration 1:

Best path: A → B → D → C
Best cost: 27
Pheromone updated: Edge yang dilalui naik jadi 4.204
Next iteration: Edge dengan pheromone tinggi lebih mungkin dipilih!

🔄 ITERATION 2 - SEMUT 1

Step 1: Dari A (Dengan Pheromone Baru)

Pheromone sekarang:

τ_AB = 4.204 (tinggi!)
τ_AC = 0.5 (rendah)

Hitung Attractiveness:

Edge	τ	η	τ¹ × η²
A-B	4.204	0.100	0.0420
A-C	0.5	0.050	0.0013

Hitung Probabilitas:

Total: 0.0420 + 0.0013 = 0.0433

P_AB = 0.0420 / 0.0433 = 0.97 (97%)
P_AC = 0.0013 / 0.0433 = 0.03 (3%)

✅ Hampir pasti pilih A-B! (pheromone tinggi)
Ini adalah efek reinforcement learning!

💡 Key Insights:

Iteration 1: P(A-B) = 80% → Pilih A-B
Update pheromone: A-B naik dari 1.0 ke 4.204
Iteration 2: P(A-B) = 97% → Hampir pasti A-B!
Konvergensi: Setelah beberapa iterasi, semua semut pilih path yang sama

🎯 Proses Belajar ACO:

Good solution → High pheromone → More ants choose it → Even higher pheromone → Convergence!

📈 Summary Calculation Table

Iteration	Path	Cost	τ_AB	τ_AC	P(A-B)
0	-	-	1.00	1.00	80%
1	A→B→D→C	27	4.20	0.50	97%
2	A→B→D→C	27	5.81	0.25	99%
3+	A→B→D→C	27	→ ∞	→ 0	→ 100%

🎯 Definisi Algoritma

1️⃣ Penjelasan Algoritma/Metode

📌 Algoritma Ant Colony Optimization (ACO)

📌 Algoritma Kruskal (untuk Minimum Spanning Tree)

2️⃣ Perbedaan Kunci: ACO-TSP vs. ACO-MST

3️⃣ Mengapa Ide-Ide Ini Muncul? (Scientific Reasoning)

💡 Design Thinking Process:

Step 1: Establish Ground Truth

Step 2: Test Basic Heuristic

Step 3: Hypothesis Testing (Parameter Tuning)

Step 4: Problem Variation (TSP vs MST)

Step 5: Real-World Constraint

4️⃣ Filosofi: Ilmu Pasti vs Ilmu Heuristik

🤔 Mengapa Perlu Ilmu Pasti di Heuristik?

5️⃣ Harapan & Future Direction

📊 Contoh Perhitungan Manual ACO Step-by-Step

🗺️ Setup: Graph Sederhana 4 Nodes

Graph:

Distance Matrix:

Parameter ACO:

🐜 ITERATION 1 - SEMUT 1

Inisialisasi

Step 1: Dari A, pilih edge berikutnya

Hitung Heuristic (η = 1/distance):

Hitung Attractiveness (τα × ηβ):

Hitung Probabilitas:

Step 2: Dari B, pilih edge berikutnya

Hitung Heuristic:

Hitung Attractiveness:

Hitung Probabilitas:

Step 3: Dari D, pilih edge berikutnya

♻️ UPDATE PHEROMONE (Setelah Semut 1)

Step 1: Evaporation (Semua Edge)

Step 2: Deposit (Hanya Edge yang Dilalui)

📊 Hasil Iteration 1:

🔄 ITERATION 2 - SEMUT 1

Step 1: Dari A (Dengan Pheromone Baru)

Hitung Attractiveness:

Hitung Probabilitas:

💡 Key Insights:

🎯 Proses Belajar ACO:

📈 Summary Calculation Table

Hitung Attractiveness (τ^α × η^β):